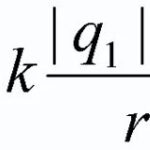La força de Lorentz i la regla de la mà esquerra. Moviment de partícules carregades en un camp magnètic

Col·locat en un camp magnètic conductorper on passava electricitat, es veu afectada per la força d'Ampere $F_A$ , i el seu valor es pot calcular mitjançant la fórmula següent:

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

on $jo$ i $l$ - Potència del corrent i longitud del conductor, $B$ - Inducció de camp magnètic, $\alpha$ - l'angle entre les direccions de la intensitat del corrent i la inducció magnètica. Per què passa això?

Força de Lorentz. Moviment d'una partícula carregada en un camp magnètic.

Contingut

1 Què és la força de Lorentz - determinar quan es produeix, obtenint la fórmula
2 Determinació de la direcció de la força de Lorentz utilitzant la regla de la mà esquerra
3 Moviment d'una partícula carregada en un camp magnètic
4 Aplicació de la força de Lorentz a l'enginyeria

Què és la força de Lorentz - determinar quan es produeix, obtenint la fórmula

Se sap que el corrent elèctric és un moviment ordenat de partícules carregades. També s'ha establert que durant el moviment en un camp magnètic, cadascuna d'aquestes partícules està sotmesa a l'acció d'una força. Perquè es produeixi una força, la partícula ha d'estar en moviment.

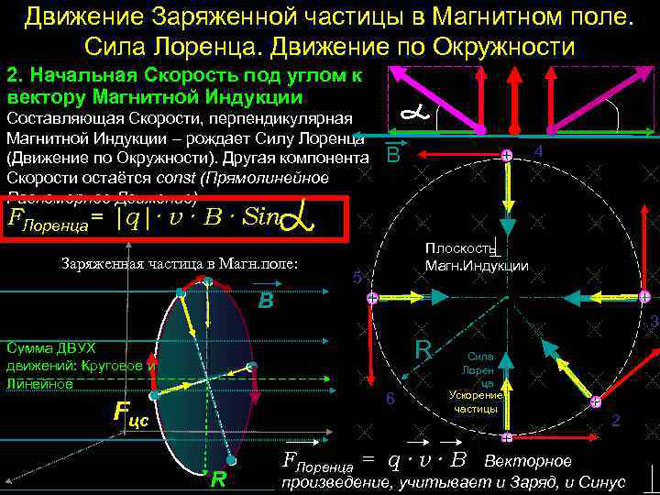
La força de Lorentz és la força que actua sobre una partícula carregada elèctricament mentre es mou en un camp magnètic.La seva direcció és ortogonal al pla en què es troben els vectors de la velocitat de les partícules i la força del camp magnètic. La resultant de les forces de Lorentz és la força d'Ampère. Sabent-ho, podem derivar una fórmula per a la força de Lorentz.

El temps necessari perquè la partícula passi pel segment del conductor, $t = \frac {l}{v}$ , on $l$ - la longitud del segment, $v$ és la velocitat de la partícula. La càrrega total transferida durant aquest temps a través de la secció transversal del conductor, $Q = I\cdot t$ . Substituint aquí el valor del temps de l'equació anterior, tenim

$Q = \frac {I\cdot l}{v}$ (2)

Al mateix temps $F_A=F_L\cdot N$ , on $N$ és el nombre de partícules en el conductor considerat. On $N = \frac {Q}{q}$ , on $q$ és la càrrega d'una partícula. Substituint el valor a la fórmula $Q$ de (2), es pot obtenir:

$N = \frac {I\cdot l}{v\cdot q}$

Per aquest camí,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Utilitzant (1), l'expressió anterior es pot escriure com

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Després de les contraccions i transferències, apareix una fórmula per calcular la força de Lorentz

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Atès que la fórmula s'escriu per al mòdul de força, s'ha d'escriure de la següent manera:

Llegeix també: Com convertir amplificadors en watts i viceversa?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Perquè el $sin\alpha = sin(180^{\circ} - \alpha)$ , aleshores, per calcular el mòdul de força de Lorentz, no importa cap a on es dirigeix la velocitat, - en la direcció de la força del corrent o en contra, - i podem dir que $\alpha$ és l'angle format pels vectors velocitat de partícula i inducció magnètica.

Escriure una fórmula en forma vectorial serà així:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\times \vec{B}]$ és un producte creuat, el resultat del qual és un vector amb mòdul igual a $v\cdot B\cdot sin\alpha$ .

A partir de la fórmula (3), podem concloure que la força de Lorentz és màxima en el cas de direccions perpendiculars del corrent elèctric i del camp magnètic, és a dir, quan $\alpha = 90^{\circ}$ , i desapareixen quan són paral·lels ( $\alpha = 0^{\circ}$ ).

Cal recordar que per obtenir la resposta quantitativa correcta, per exemple, quan es resolen problemes, s'han d'utilitzar les unitats del sistema SI, en què la inducció magnètica es mesura en tesles (1 T = 1 kg s).⁻²·PERÒ⁻¹), força - en Newtons (1 N = 1 kg m/s²), intensitat del corrent - en amperes, càrrega en coulombs (1 C = 1 A s), longitud - en metres, velocitat - en m / s.

Determinació de la direcció de la força de Lorentz utilitzant la regla de la mà esquerra

Com que la força de Lorentz es manifesta com la força d'Ampère al món dels macroobjectes, la regla de la mà esquerra es pot utilitzar per determinar la seva direcció.

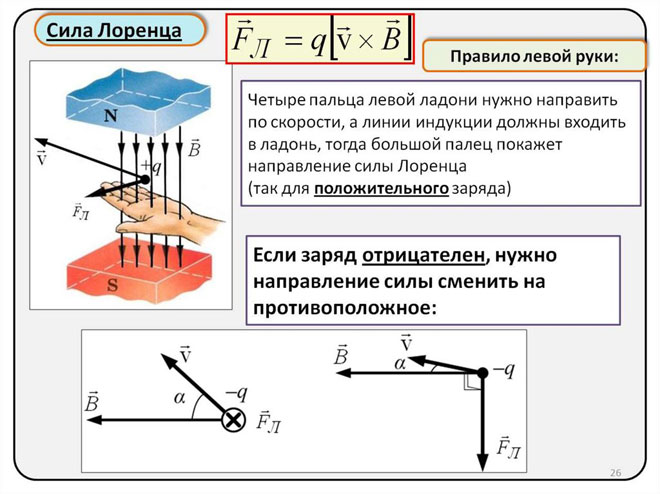
Determinació de la direcció d'acció de la força de Lorentz segons la regla de la mà esquerra.

Heu de posar la mà esquerra de manera que el palmell obert sigui perpendicular i cap a les línies del camp magnètic, quatre dits s'han d'estendre en la direcció de la força actual i, a continuació, la força de Lorentz es dirigirà cap a on apunta el polze, que s'ha de doblegar.

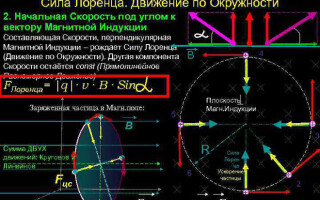
Moviment d'una partícula carregada en un camp magnètic

En el cas més simple, és a dir, quan els vectors d'inducció magnètica i velocitat de partícules són ortogonals, la força de Lorentz, en ser perpendicular al vector velocitat, només pot canviar la seva direcció. La magnitud de la velocitat, per tant, i l'energia es mantindran sense canvis. Això vol dir que la força de Lorentz actua per analogia amb la força centrípeta en mecànica, i la partícula es mou en cercle.

Llegeix també: Quants watts hi ha en un quilowatt?

D'acord amb la llei de Newton II ( $F = m\cdot a$ ) podem determinar el radi de gir de la partícula:

$N = \frac {m\cdot v}{q\cdot B}$ .

Cal tenir en compte que amb un canvi en la càrrega específica de la partícula ( $\frac {q}{m}$ ) el radi també canvia.

En aquest cas, el període de rotació T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . No depèn de la velocitat, la qual cosa significa que la posició mútua de partícules amb diferents velocitats no canviarà.

Moviment d'una partícula carregada en un camp magnètic uniforme.

En un cas més complicat, quan l'angle entre la velocitat de la partícula i la força del camp magnètic és arbitrari, es mourà al llarg d'una trajectòria helicoïdal, en translació a causa del component de velocitat dirigit paral·lel al camp, i al llarg del cercle sota la influència de la seva component perpendicular.

Aplicació de la força de Lorentz a l'enginyeria

Cinescopi

El cinescopi, que es va mantenir fins fa poc, quan va ser substituït per una pantalla LCD (plana), a tots els televisors, no podria funcionar sense la força de Lorentz. Per formar un ràster de televisió a la pantalla a partir d'un corrent estret d'electrons, s'utilitzen bobines deflectores, en les quals es crea un camp magnètic que canvia linealment. Les bobines horitzontals mouen el feix d'electrons d'esquerra a dreta i el tornen enrere, les bobines de personal són les responsables del moviment vertical, movent el feix horitzontalment de dalt a baix. S'utilitza el mateix principi oscil·loscopis - aparells utilitzats per estudiar la tensió elèctrica alterna.

espectrògraf de masses

Un espectrògraf de masses és un dispositiu que utilitza la dependència del radi de rotació d'una partícula carregada de la seva càrrega específica. El principi del seu funcionament és el següent:

La font de partícules carregades, que agafen velocitat amb l'ajuda d'un camp elèctric creat artificialment, es col·loca en una cambra de buit per tal d'excloure la influència de les molècules d'aire. Les partícules surten volant de la font i, després d'haver passat per l'arc de cercle, xoquen contra la placa fotogràfica, deixant-hi rastres. En funció de la càrrega específica, canvia el radi de la trajectòria i, per tant, el punt d'impacte. Aquest radi és fàcil de mesurar, i coneixent-lo, es pot calcular la massa de la partícula. Amb l'ajuda d'un espectrògraf de masses, per exemple, es va estudiar la composició del sòl lunar.

Llegeix també: Quines són les professions relacionades amb l'electricitat

Ciclotró

La independència del període, i per tant la freqüència de rotació d'una partícula carregada de la seva velocitat en presència d'un camp magnètic, s'utilitza en un dispositiu anomenat ciclotró i dissenyat per accelerar les partícules a altes velocitats. Un ciclotró són dos mitges cilindres de metall buits: un dee (de forma, cadascun d'ells s'assembla a la lletra llatina D) col·locats amb els costats rectes entre si a poca distància.

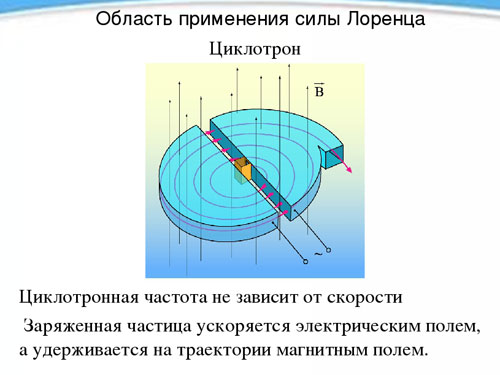
Ciclotró: aplicació de la força de Lorentz.

Els dees es col·loquen en un camp magnètic uniforme constant i es crea un camp elèctric altern entre ells, la freqüència del qual és igual a la freqüència de rotació de la partícula, determinada per la força del camp magnètic i la càrrega específica. Arribant dues vegades durant el període de rotació (durant la transició d'un dee a un altre) sota la influència d'un camp elèctric, la partícula s'accelera cada vegada, augmentant el radi de la trajectòria i, en un moment determinat, havent guanyat la velocitat desitjada, vola fora del dispositiu pel forat. D'aquesta manera, un protó es pot accelerar a una energia de 20 MeV (megaelectronvolt).

Magnetró

Un dispositiu anomenat magnetró, que s'instal·la en cadascun microones, és un altre representant dels dispositius que utilitzen la força de Lorentz. El magnetró s'utilitza per crear un potent camp de microones, que escalfa el volum intern del forn, on es col·loca el menjar. Els imants inclosos en la seva composició corregeixen la trajectòria del moviment dels electrons a l'interior del dispositiu.

Camp magnètic terrestre

I a la natura, la força de Lorentz té un paper extremadament important per a la humanitat. La seva presència permet que el camp magnètic de la Terra protegeixi les persones de la radiació ionitzant mortal de l'espai. El camp no permet que les partícules carregades bombardin la superfície del planeta, obligant-les a canviar de direcció.

Articles semblants: